6 Unproductive Ways to Learn Math Basics—and What to Do Instead
Tune up your math teaching with this review of strategies to avoid, plus alternatives that will challenge, engage, and enlighten your students.
When it comes to teaching math basics, a lot of progress has been made in the way we approach key skills like number sense, but there are some older, less productive practices still making the rounds. Too often, young students are introduced to foundational concepts like addition, multiplication, fractions, and subtraction—their first brush with formal mathematics—using tactics that prioritize speed, memorization, automaticity, and, above all, right answers and accuracy.
Right answers matter, of course, and speed, recall, and automaticity underlie long-term fluency, but none of it should come at the expense of mathematical reasoning and procedural (as opposed to factual) fluency, according to the researchers Gina Kling, a mathematics teacher educator at Western Michigan University, and Jennifer Bay-Williams, a professor of mathematics education at the University of Louisville. In a 2021 study, they suggest that many common teaching practices send the message that math is essentially about recall and blind adherence to formulas. Instead, it’s our responsibility to bring math to life, they say, by designing learning experiences that emphasize “curiosity, flexibility, and wonder” and position mathematics as a powerful, adaptable tool for making sense of the world.
“Long-standing methods for teaching basic facts have not been effective for far too many students,” explain Kling and Bay-Williams, who point to “quick fix” approaches that actually hinder math learning, sacrificing a young student’s long-term development of number sense in favor of short-term tasks that emphasize rote memorization and speed. The tactics can produce anxiety and long-term math avoidance starting as early as first grade, according to a 2013 study.
Here are six unproductive math practices that teachers should avoid.
1. Ignoring visualization strategies
It’s a faulty assumption that you can explain a math strategy verbally and students will get it—but educators “cannot simply tell a student to understand,” Kling and Bay-Williams write. More important, students need time and experiences to understand and visualize number relationships, not just a good explanation.
Make liberal use of visual strategies, the researchers say. One fun activity is to use Quick Look cards: Briefly show students groups of several dots—or photos of familiar items like a carton of eggs—and then ask them how many they saw and how they saw them. For example, did students see four groups of two or two groups of four? Seeing numbers represented visually, whether with dots or manipulatives, can help students gain a better understanding of how and why math strategies work.
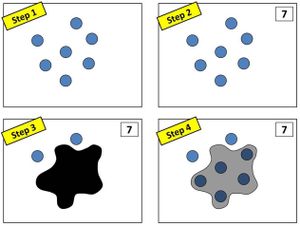
Or you could try Splat!, designed by Steve Wyborney, a K–12 district math coach in Oregon. Using a series of slides, he first asks his students to count the number of dots they see. He then shows the next slide, which suddenly has a large amoeboid blob covering several dots, and asks, “How many dots have been covered by the splat?” Students often come up with their own strategies—whether counting up or down, or using their voice or fingers.
2. Teaching math facts in numerical order
A common approach is to teach addition and multiplication facts in order of addend or factor size—starting with 0s, and then moving to 1s, then 2s, and 3s, for example, when learning the times tables. But that’s a mistake, because students then tend to see mathematical “facts as isolated objects,” write Kling and Bay-Williams, which can result in a superficial understanding of mathematical operations and ultimately reduce a student’s level of achievement.
They point to research showing that starting with foundational sets—2s, 10s, and 5s—is not only more familiar to students but also vital because other math facts can be derived from them. For example, once a student learns their 5s, they can break down challenging problems—such as 8 x 7—into 8 x 5 plus 8 x 2, and also tackle more daunting problems like 56 x 8. After mastering the foundational sets, students should move on to squares (7 x 7) “because some of the toughest facts to learn (e.g., 7 × 8 and 6 × 7) are close to squares, and squares are useful for later work in algebra, geometry, and measurement.”
3. Sticking with one strategy to solve problems
When students first learn subtraction, they’re often taught to convert the problem into an addition problem. For example, if they’re solving 15 – 9 = ?, they’d start with 9 and think about what they should add to reach 15. This is a good approach, but it’s just one strategy out of many, and ignoring the others can inhibit a student’s ability to develop richer number reasoning skills.
Get students to mix in other strategies like compensation—converting 15 – 9 into 15 – 10 and then adding 1 to the answer, for example. Students should also learn how to break apart the minuend (the number to be subtracted from) and subtrahend (the number to be subtracted). For example, in the original 15 – 9 problem, you can break the 15 into 10 and 5, and show students that they can first solve 10 – 9, and then add the remainder of 5 to arrive at the final answer of 6.
Once students have a grasp of compensation and breaking down numbers, they can move up the scale to larger numbers, such as 132 – 99, which is the same as 132 – 100 = 32, and then adding 1. Using multiple strategies supports mathematical sense-making that goes far beyond the immediate math problem.
4. Focusing too much on fact mastery and recall
Pages densely packed with math problems send the message to students that speed and mechanical mastery are more important than developing a robust sense of math fluency. “Very few students want to do 30+ problems on a page,” write Kling and Bay-Williams, and that first bad taste “leads many students to decide they do not like mathematics.”
Similarly, placing too much emphasis on memorization and calculation tricks—such as teaching young learners how to quickly multiply by 9 using their fingers—doesn’t help with other numbers. While it may be a useful starting point, it’s better to help students develop fluency by teaching them reasoning strategies. For example, 69 + 58 might seem daunting to solve, but teaching students how to “make tens”—by adding 1 to 69 and subtracting 1 from 58, transforming the problem into 70 + 57—helps them learn how to manipulate numbers more fluidly.
You can also spice things up with hands-on games and interactive activities: Math games such as bingo addition and connect four reveal how comfortable students are with applying different mathematical strategies—such as breaking numbers down and estimating—and the reasoning behind their answers, which can greatly increase students’ taste for math.
5. Placing too much emphasis on speed
Speed contests such as board races and timed online games are fun and can help young learners practice how to add, subtract, and multiply quickly—but consider using them sparingly.
That’s because emphasizing speed too early can “drive fluency development in the opposite direction,” explain Kling and Bay-Williams, encouraging students to revert to simple strategies that can be executed fast, like counting, instead of practicing more complex, time-consuming strategies that build flexible mathematical reasoning skills.
Balance speed with reflection and mix in fun, low-stress games that help students practice their math skills in a variety of ways. For example, a favorite is Tens Go Fish, in which players look for combinations of two cards that add up to 10, instead of matching pairs (so if a student has a 7 in their hand, they can ask their opponent for a 3).
6. Adding extra pressure through timed tests
Math fluency can be stymied when students are forced to finish single-answer math tests quickly, like “asking third graders to solve 100 multiplication problems in three minutes,” write Kling and Bay-Williams. While timed tests can sometimes be used as quick assessments of fluency, they are poor ways to measure flexible thinking—a hallmark of strong mathematical reasoning—and can also cause anxiety, inhibit clear thinking, unfairly penalize methodical thinkers, and reinforce the idea that mathematics is a dreary, unforgiving discipline.
Try using a range of assessment strategies, such as think-pair-share, peer interviews, journaling, open-ended questions, and storytelling instead, which don’t have the pernicious effects of timed tests while offering a more accurate picture of what students know. Following up a math problem with “How did you figure it out?” places less emphasis on getting the right answer and communicates to students that their thinking matters.
Source: https://www.edutopia.org/article/6-unproductive-ways-learn-math-basics-and-what-do-instead